5 - Notions statistiques

Introduction

Les statistiques désignent un ensemble de règles et de procédures permettant de résumer des grands ensembles de données en ensemble que l’on pourra traiter plus facilement. Elles permettent également de tirer des conclusions à partir de ces données.

Les procédures statistiques se divisent en deux catégories : les statistiques descriptives ou déductives et les statistiques inférentielles ou inductives. Le principe général de l’expérimentation est simple : on fait passer des expériences aux sujets dans lesquelles on fait varier des variables indépendantes. Les différences observées quant au comportement du sujet reflètent l’influence des variables indépendantes.

Les rôles des statistiques

L’écriture des résultats

Les statistiques descriptives permettent de résumer les résultats afin de faire ressortir l’essentiel. Elles consistent en la présentation des données sous forme de tableaux, de graphiques et de calcul des valeurs résumant les données d’un échantillon.  (moyenne, écart type).

Estimer

Les statistiques sont également employées pour estimer la validité des résultats. La statistique inférentielle atteste de la solidité des conclusions à l’issue de l’analyse descriptive. Elle cherche à généraliser à l’ensemble de la population, les résultats obtenus par des échantillons de cette population.

Les statistiques permettent donc de prédire les comportements humains, non pas avec une certitude totale mais avec une chance entre 1 et 5 de se tromper sur 100.

Les statistiques descriptives

Objectifs

Une analyse descriptive vise à décrire numériquement la distribution des données sans en tirer de conclusion pour une population plus grande. On a recours à des représentations graphiques pour résumer les données brutes.

Les points essentiels à apparaître

• La distribution des données

On utilise un histogramme afin de présenter les données individuelles.

• Les mesures des tendances centrales

Leurs objectifs est de trouver une valeur numérique qui représente au mieux le centre d’une distribution. Elles permettent d’obtenir la position où semblent se rassembler les valeurs de la série. La moyenne, par exemple, prend en compte quantitativement l’ensemble des valeurs individuelles.

La moyenne se définit comme la somme des valeurs individuelles obtenues divisée par leur nombre total. Attention, la moyenne n’est pas toujours significative car on peut obtenir une même moyenne pour des résultats différents. On constate donc la nécessité de ne pas se limiter au calcul de la tendance centrale mais de prendre aussi en compte la dispersion qui existe autour de la moyenne. Si la dispersion est importante, la moyenne a peu de sens. De ce fait, on ne peut prédire qu’en répliquant l’expérience.

• La suite de résultats

Elle donne la répartition des résultats de façon visuelle. L’histogramme est constitué de rectangles de hauteur proportionnelle à l’effectif.

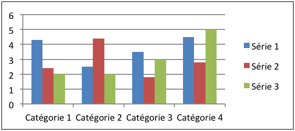
• Mesure de la dispersion

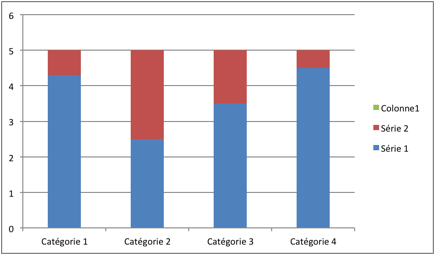
Ici, la moyenne m(x) est de 5. La dispersion (en rouge) se calcule comme la somme des différences entre le résultat de chaque série avec la moyenne (Xi – m).

La variance se calcule avec la formule suivante :

Var =

La dispersion s(x) se calcule alors ainsi :

S(x) =

Si la dispersion est grande, la moyenne n’est pas significative. La variance et la dispersion traduisent des évolutions dites aléatoires causées par le ‘bruit’, c’est-à-dire l’ensemble des différences inter-individuelles ou encore la non constance individuelle.

Par contraste, on trouve l’évolution systématique qui est due à la variable manipulée. Plus la dispersion est proche de 0, plus l’effet constaté reflète l’impact de la variable indépendante. Plus elle est éloignée de 0, plus l’expérimentation doit être remise en cause.

Les représentations des mesures

Les données sont présentées dans un tableau où figure, pour chaque modalité de la variable indépendante, la moyenne et la dispersion. On distinguera les données brutes des tableaux en annexe.

• Les tableaux

• Le titre se situe au-dessus du tableau avec son label toujours écrit de la façon suivante : variable dépendante obtenue en fonction de la variable indépendante.
• Les tableaux sont numérotés en fonction de leur ordre d’apparition dans le texte, indépendamment des figures.
• Seul le titre est souligné, non le label.
• Une légende est éventuellement écrite en note en-dessous du tableau. Note est souligné.

• Les figures

Les figures donnent une image parlante aux résultats. Par convention, la variable dépendante est représentée sur l’axe des ordonnées, la variable indépendante sur l’axe des abscisses.

• Le titre est placé en-dessous de la figure
• Les figures sont numérotées dans l’ordre d’apparition dans le texte
• Seul le label est souligné
• Le titre s’exprime tel que la variable dépendante est donnée en fonction de la variable indépendante
• Les points sont joints

Les statistiques inférentielles

Faire des inférences statistiques, c’est comparer le poids des sources d’évolutions systématiques au poids des évolutions aléatoires. Un échantillon n’est jamais la réplique exacte de la population dont il provient, de même, les données varient toujours d’un échantillon à un autre.

Les techniques inférentielles ont été développées pour isoler la variabilité systématique (due aux facteurs expérimentaux) de la variabilité aléatoire (notée par la dispersion). Le but de cette analyse est donc d’observer si l’effet constatée est dû à la variable manipulée (dans ce cas, on peut généraliser) ou au contraire, s’il est dû à la variable aléatoire (dans ce cas, on ne peut rien conclure).

Pour généraliser, on ne peut qu’utiliser les statistiques inférentielles car on ne peut refaire les expériences un nombre élevé de fois, tout comme on ne peut faire passer les expériences à l’ensemble de la population.